How to follow along

Two basic docker commands are required to follow along with this lesson -

docker pull learnreverseengineering/lesson5
docker run -it --cap-add=SYS_PTRACE --security-opt seccomp=unconfined learnreverseengineering/lesson5 bash

Introduction

I imagine that it probably seems a little silly (or daunting) that there is a lesson dedicated solely to PEMDAS (and a couple of bonus bits and pieces). ASM approaches PEMDAS operations in a more convoluted manner than high level languages, and some operations (specifically division and multiplication) have some intricacies that seemed worthy of putting into this mathematics-focused lesson!

On the subject of PEMDAS, ASM doesn't actually have parentheses, so we're actually just going to cover EMDAS. ASM also doesn't have any annoying ambiguity on the order of mathematical operations, because the instructions are simply executed sequentially in the order that they're written... so EMDAS isn't actually even applicable here. 🤔

Addition

Addition, the easiest operation of the whole bunch. The instruction is ADD DESTINATION, SOURCE where destination can be either a register or a stack location, and source can be a register, a stack location or a constant value.

The instruction looks as follows in practice -


        ; Put 40 into RAX
        mov RAX, 40
        ; put 40 into RBX
        mov RBX, 40
        ; Add them together
        add RBX, RAX
        ; RBX is now 80, RAX is still 40
        ; Add 50 to RAX's value
        add RAX, 50
        ; RAX is now 90

Very straightforward, onto the next one.

Subtraction

Subtraction is just as straight forward as addition. Same instruction structure, SUB DESTINATION, SOURCE. Once again the destination can be a register or a stack location and the source can be a register, a stack location or a constant value.

A quick example:


        ; Put 800 into RAX
        mov RAX, 800
        ; put 350 onto the stack
        mov qword ptr [RBP-0x10], 350
        ; Subtract that value from RAX
        sub RAX, qword ptr [RBP-0x10]
        ; RAX is now 450, the stack location is still 350
        sub RAX, 50
        ; RAX is now 400

Nice.

Multiplication

This is where things begin to get a little weird though unfortunately (and they get weirder in Division ).

Unlike addition and subtraction, multiplication can be performed in three different ways.

MUL SOURCE
IMUL DESTINATION, SOURCE
IMUL DESTINATION, SOURCE1, SOURCE2

MUL SOURCE

This instruction multiplies the contents of the RAX register (always RAX, this is unchangeable) with the contents of SOURCE, where source can be a constant, a register value or a stack location. For example:


        mov RAX, 20
        mov RDI, 2
        mul RDI
        ; At this point RAX is 40 (20*2) and RDI is still 2.
        ; In a high level language this is equivalent to int RAX = 20; int RDI = 2; RAX *= RDI

IMUL DESTINATION, SOURCE

This instruction is getting closer to what we'd typically expect multiplication to look like. We are able to supply which register is going to be modified by the multiplication operation. For example:


        mov RAX, 1
        mov RCX, 53
        imul RCX, 3
        ; At this point RCX is 159 (53*3) and RAX is still 1.
        ; In a high level language this is equivalent to int RAX = 1 ; int RCX  = 53 ; RCX *= 3;

IMUL DESTINATION, SOURCE1, SOURCE2

This instruction is probably what most people think of when they think about the multiplication operation. We have complete control over the values which are multiplied together and where the result is placed. For example:


        mov RAX, 20
        mov RBX, 10
        mov RCX, 30
        imul RAX, RBX, RCX
        ; At this point RAX is 300, RBX and RCX remain unchanged.
        ; In a high level language this is equivalent to int RAX = 20 ; int RBX = 10 ;  int RCX  = 30 ; RAX = RBX * RCX;

Clearly the last instruction is the most versatile of the bunch, but you'll see every one of these during your reverse engineering adventures.

Division

Division in x86 and x64 ASM is unintuitive and idiosyncratic, there's just no way around it unfortunately. Dividing in Intel ASM causes there to be some collateral effects on other registers (which I suppose is helpful in that it prevents us from having to worry about floating point numbers, as we'll see shortly)

The most basic case, as with multiplication is idiv SOURCE_VALUE. With this form of the IDIV instruction, whatever is in RAX (hardcoded, unchangeable) is divided by whatever is in SOURCE_VALUE (which can be a register, stack location or constant.)


        mov RAX, 14
        mov RBX, 2
        idiv RBX
        ; RAX becomes 7, RBX stays as 2
        ; This is equivalent in C to "int RAX = 14; int RBX = 2; RAX = RAX / RBX;"

The wheels immediately fall off though in the case where the dividend isn't evenly divisible by the divisor..


        mov RAX, 13
        mov RBX, 2
        idiv RBX
        ; RAX becomes 6, RBX is still 2 and RDX becomes 1

RDX essentially contains the 'remainder' of the integer division, the bit which couldn't be evenly divided.

It gets even weirder though, because if we try to perform any other subsequent division operation without manually setting RDX to zero then the application will crash. This is demonstrated in /lesson/crashyDivisionAsm in the lesson's Docker container -

crashyDivision.asm:


        section .text
        extern exit
        global _start, main

        main:
        _start:
            ; Firstly, setup some registers
            mov RAX, 13
            mov RBX, 2
            idiv RBX

            ; RAX is now 6, RBX is 2, RDX is 1

            mov RAX, 12
            idiv RBX ; We will crash here because RDX isn't explicitly cleared

            mov RDI, 0 ; exit code will be '0'
            call exit ; quit the app

The result when executed in GDB: SIGFPE from trying to divide uncleanly without clearing RDX first.

In order to avoid the above situation, simply clear down RDX prior to subsequent divisions using either mov rdx, 0 or xor rdx, rdx (this one's a little fancy, it's exclusive-ORing the register with itself, which is a fast way of clearing a register to 0).

It should be noted that while there are three instructions available to perform multiplication, there is only one instruction to perform division.

Exponents

So at this point, you're probably thinking "Cool, I bet there's an EXP instruction or a POW instruction to raise numbers to different powers!".

Well, you'd be incorrect. x64 Intel ASM doesn't natively support exponential operations on numbers, and neither does the C language, so those things need to be coded manually using either loops or binary maths or by using math.h's pow() function.

Because the pow() function takes a double as an argument (which we haven't covered yet), and because we haven't covered loops yet (we will in two lessons time) and because we haven't covered binary maths yet (we will next lesson), I'm simply going to skip over exponents for now like a coward.

There's some C code inside of the container under /lesson/exponent.c which you can look at to get an idea of how it's done in C, and if you're feeling brave enough then you can disassemble /lesson/exponent in GDB to get an idea of how floating point numbers look in assembly (please don't be discouraged if you don't understand it, floats in ASM are like black magic and we will get there soon.

Honorable mentions

There are two other instructions which are tangentially mathematics-related which pop up frequently during reverse engineering, inc REGISTER and dec REGISTER. These instructions are super simple, they both take a register as an argument and either decrement it or increment it accordingly.

A basic example -


        mov rax, 25
        dec rax
        ; rax is now 24
        inc rax
        ; rax is now 25 again
        dec rax 
        dec rax 
        dec rax 
        ; rax is now 22. You get it I'm sure.

A complete reverse engineering exercise

OK at this point we understand 4 / 5 elements of PEMDAS, so we're in good shape to start reverse engineering something a little more interesting. The disassembly for this code is going to be fairly large but repetitive, so don't be disheartened if it looks scary at first - if you've read all of the previous lessons then it's perfectly manageable.

The code, available under /lesson/challenge.c in the container, is as follows -


        #include <stdio.h>
            
            int main(int argc, char** argv) {
                long challengeNumber = 1;
                long secondaryNumber = 2;
                challengeNumber = challengeNumber + 25;                 // this should generate an ADD instruction
                challengeNumber = challengeNumber - 2;                  // this should generate a SUB instruction
                secondaryNumber = challengeNumber * 2;                  // this should generate an IMUL instruction
                challengeNumber *= 331;                                 // Another IMUL instruction
                challengeNumber = challengeNumber / secondaryNumber;    // and finally an IDIV instruction
                printf("The final number is %li\n", challengeNumber);   // Print the result
            }

Pretty straightforward code when you can see the high level language representation of it. Let's look at the ASM in GDB -

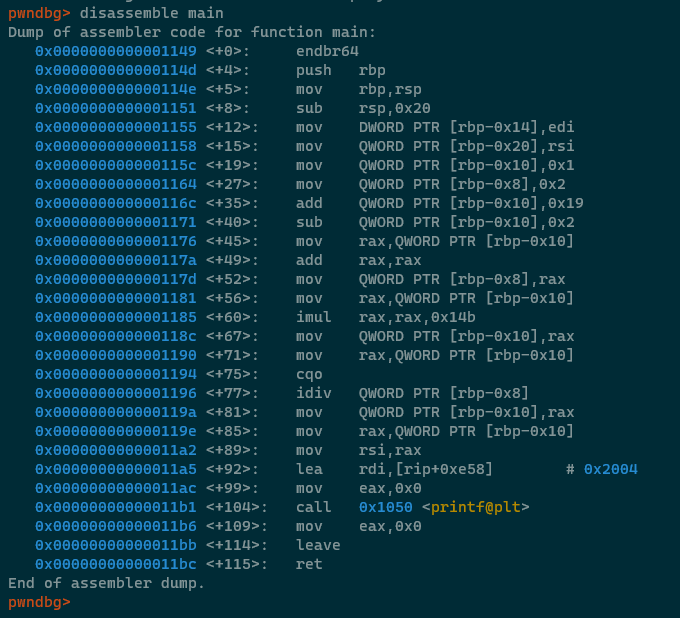
The assembly code of the main method of the challenge binary

As discussed above, this might initially look a little daunting and frustrating, but literally all of the building blocks which we've discussed are there!

add QWORD PTR [rbp-0x10],0x19 is "challengeNumber = challengeNumber+25"
sub QWORD PTR [rbp-0x10],0x2 is "challengeNumber = challengeNumber -2"
add rax, rax is an elegant optimization which multiplies RAX by 2 (number + number is the same as number * 2, after all)
imul rax,rax,0x14b is "challengeNumber *= 331", multiplying challengeNumber by 0x14b (331 decimal)
idiv QWORD PTR [rbp-0x8] is "challengeNumber = challengeNumber / secondaryNumber;"

Not as intimidating as it initially appears, I hope. The bulk of the disassembly is MOV instructions putting data into the correct places to perform the mathematical operations.

One instruction is new to us though, and we should discuss it - CQO. The manual says that "The CQO instruction (available in 64-bit mode only) copies the sign (bit 63) of the value in the RAX register into every bit position in the RDX register.". In reality, this simply has the effect of clearing the RDX register back to zero before the division operation, which helps to prevent the SIGFPE error seen above!

Conclusion

I hope that this lesson has been interesting and manageable, there are just a few lessons left now until we understand enough about the fundamentals of ASM to start working through some reverse engineering lessons! If you're working through these lessons sequentially then keep it up, you're doing great!

Lesson 5 - How arithmetic is implemented in ASM.