How to follow along
Two basic docker commands are required to follow along with this lesson -
docker pull learnreverseengineering/lesson9docker run -it --cap-add=SYS_PTRACE --security-opt seccomp=unconfined learnreverseengineering/lesson9 bash
Introduction
This lesson will act as an introduction to the topic of floating point numbers, and how they're represented/manipulated in the x64 ASM language. This topic required its own lesson because ASM has some confusing and frustrating idiosyncrasies around floating point numbers, and it felt right to have a specific lesson for the topic.
Full disclosure, I've been dreading writing up this lesson because floats are painful in my opinion.
What's a floating point number?
A floating point number, henceforth referred to as a float is a high precision number which isn't a
whole integer. A classic example of a float is PI. PI is 3.14159265359...., there is no way to
represent this level of precision inside of a high level language's int data type, so two special
data types were contrived called float and double. A float can represent up to 32
bytes (4 bytes) worth of precision on a decimal number (huge, of course), a double can represent double
that precision, up to 64 bits (8 bytes).
For situations where precision is paramount, use double. For situations where precision (or even just the number of decimal places) isn't really too much of an issue, use float.
How are floats represented in ASM?
So we've covered how integers are represented in ASM at great length over the past 8 lessons. The number '1' is represented as 0x0000000000000001 in a register. The letter 'A' is represented as 0x0000000000000041. The number '2863311530' is represented as 0x00000000AAAAAAAA. This is all very neat, each of the general purpose registers (and the stack) can represent these values with no issue at all.
The wheels fall off quite dramatically though when we need to represent, for example, 1.234. It doesn't fit neatly into a register like 0x00001.234 unfortunately.
Instead, x64 ASM makes use of 16 special registers in our CPU which are purpose built for holding and manipulating floating point data. They are named XMM0 to XMM15.
The CPU extension which added these registers in the late 90s was called Streaming SIMD Extension (SSE). Wikipedia has an excellent article on these registers (and the history behind them).
The XMM* registers are all 128 bits wide, which means that they are able to accommodate -
- 4 floats (4*32 bits) OR
- 2 doubles (2*64 bits) OR
- 16 bytes OR
- 4 ints OR
- 2 longs OR
- 1 int128 (128 bit integer)
That last point above is absolutely mindblowing. This means that any of the XMM* registers could hold up to the number 170,141,183,460,469,231,731,687,303,715,884,105,72. You can verify this information in GDB by running info registers sse or i r sse -
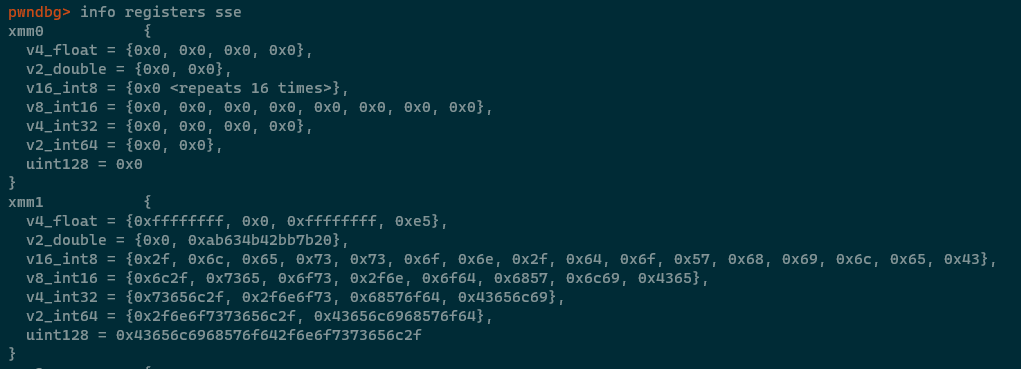
Observe how GDB helpfully tries to represent what the values might be in the register's "vectors". GDB doesn't know whether the register holds a float, a double, an int128 so it just tries to show you everything and you, as a reverse engineer, can work out what's going on.
A basic example
Let's look at a concrete example, located in the lesson's docker container under /lesson/basicFloat.c and /lesson/basicFloatCompiled
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char** argv) {
float deliciousPI = 3.1415927f;
float deliciousPI2 = 6.2831854f;
printf("The truncated value of PI is %f and PI2 is %f\n", deliciousPI, deliciousPI2);
exit(0);
}
OK, so, we have two floats. PI and PI doubled (I deliberately didn't just write PI*2 in the code
because it would have generated a floating point multiplication instruction and we're just looking at the basics
right now.). The two floats are passed as arguments to printf() which will print them to the
terminal. Simple right?
Here's the corresponding ASM code for this program -
pwndbg> disassemble
Dump of assembler code for function main:
=> 0x0000555555555169 <+0>: endbr64
0x000055555555516d <+4>: push rbp
0x000055555555516e <+5>: mov rbp,rsp
0x0000555555555171 <+8>: sub rsp,0x20
0x0000555555555175 <+12>: mov DWORD PTR [rbp-0x14],edi
0x0000555555555178 <+15>: mov QWORD PTR [rbp-0x20],rsi
0x000055555555517c <+19>: movss xmm0,DWORD PTR [rip+0xeb4] # 0x555555556038
0x0000555555555184 <+27>: movss DWORD PTR [rbp-0x8],xmm0
0x0000555555555189 <+32>: movss xmm0,DWORD PTR [rip+0xeab] # 0x55555555603c
0x0000555555555191 <+40>: movss DWORD PTR [rbp-0x4],xmm0
0x0000555555555196 <+45>: cvtss2sd xmm1,DWORD PTR [rbp-0x4]
0x000055555555519b <+50>: cvtss2sd xmm0,DWORD PTR [rbp-0x8]
0x00005555555551a0 <+55>: lea rdi,[rip+0xe61] # 0x555555556008
0x00005555555551a7 <+62>: mov eax,0x2
0x00005555555551ac <+67>: call 0x555555555060 <printf@plt>
0x00005555555551b1 <+72>: mov edi,0x0
0x00005555555551b6 <+77>: call 0x555555555070 <exit@plt>
End of assembler dump.
OK so there are two elephants in the room which I'd like to discuss. Two lines at main+19 and main+32 contain
DWORD PTR [rip+0xeb4] and DWORD PTR [rip+0xeab]. You might be thinking to yourself
"But RIP is the instruction pointer, which changes every time an instruction executes.. why is it pointing to
data?". This is something called "RIP Relative Addressing".
RIP Relative addressing is used to refer to sections in the executable outside of the section where code resides (called the .text section, by the way). The compiler establishes how far away the constant will be from the RIP register at the time of execution and inserts the correct offset. This prevents the compiler from having to hardcode an address like 0x5555555560008 into the code, which would cause problems when used with technologies like ASLR. No matter where the application is loaded in memory, the constant will always be 0xeb4 bytes from RIP at the time of execution.
Basically, the two lines can be translated as "At the time that this instruction executes, RIP will be 0xeb4 bytes away from a piece of data that we'd like to put into the XMM0 register. GDB has helpfully highlighted what that address will be at the time that the instructions will execute, 0x555555556038 and 0x55555555603c respectively. If we print the floats (with /f) at those two addresses then we'll see what's occurring -
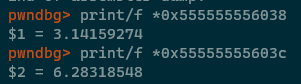
So we can see that those two RIP relative values are just PI and PI*2 which are hardcoded as constants within our application. We can use the info files command to see where those constants live within the executable too -
pwndbg> info files
Symbols from "/lesson/basicFloatCompiled".
Native process:
Using the running image of child process 16.
While running this, GDB does not access memory from...
Local exec file:
`/lesson/basicFloatCompiled', file type elf64-x86-64.
Entry point: 0x555555555080
0x0000555555554318 - 0x0000555555554334 is .interp
0x0000555555554338 - 0x0000555555554358 is .note.gnu.property
0x0000555555554358 - 0x000055555555437c is .note.gnu.build-id
0x000055555555437c - 0x000055555555439c is .note.ABI-tag
0x00005555555543a0 - 0x00005555555543c4 is .gnu.hash
0x00005555555543c8 - 0x0000555555554488 is .dynsym
0x0000555555554488 - 0x0000555555554511 is .dynstr
0x0000555555554512 - 0x0000555555554522 is .gnu.version
0x0000555555554528 - 0x0000555555554548 is .gnu.version_r
0x0000555555554548 - 0x0000555555554608 is .rela.dyn
0x0000555555554608 - 0x0000555555554638 is .rela.plt
0x0000555555555000 - 0x000055555555501b is .init
0x0000555555555020 - 0x0000555555555050 is .plt
0x0000555555555050 - 0x0000555555555060 is .plt.got
0x0000555555555060 - 0x0000555555555080 is .plt.sec
0x0000555555555080 - 0x0000555555555235 is .text
0x0000555555555238 - 0x0000555555555245 is .fini
0x0000555555556000 - 0x0000555555556040 is .rodata
..... snipped .....
The constants both reside within the .rodata (Read Only Data) section of the executable, which is a small section responsible for holding constant values! I hope that that clears those two things up slightly.
Onwards with the analysis. movss xmm0,DWORD PTR [rip+0xeb4], this is a new instruction for us which
stands for Move Scalar Single [precision], it has the effect of putting a float value (PI in this case) into the
xmm0 register. movss DWORD PTR [rbp-0x8],xmm0 performs the same operation, but copies it from XMM0
to the stack this time (for reasons that will become clear soon).
Most of the assembly floating point instructions will use confusing and scary letters
like 'ss' and 'sd' in seemingly random positions. These letters always correspond with "scalar single
precision", AKA a float and "scalar double precision", AKA a double. The more you
know. 🌈
Next up we have movss xmm0,DWORD PTR [rip+0xeab] and movss DWORD PTR [rbp-0x4],xmm0
which takes our deliciousPI2 variable from the .rodata section, places it into XMM0 and then places
it onto the stack at stackframe offset 4.
At this point XMM0 contains deliciousPI2, and the stack contains deliciousPI and
deliciousPI2.
The next two instructions are pretty obviously terrifying to a newcomer.
cvtss2sd xmm1,DWORD PTR [rbp-0x4] ; cvtss2sd xmm0,DWORD PTR [rbp-0x8]. The cvtss2sd
instruction stands for "Convert Scalar Single to Scalar Double. This has the effect of promoting (expanding) a
single precision value (a float) to a double precision value (a double). After these two instructions, if we
print the contents of XMM1 and XMM0 we'll see that they now contain double values instead of float values!
pwndbg> p/f $xmm0
$5 = {
v4_float = {3.68934881e+19, 2.142699, 0, 0},
v2_double = {3.1415927410125732, 0},
v16_int8 = {0, 0, 0, 96, -5, 33, 9, 64, 0, 0, 0, 0, 0, 0, 0, 0},
v8_int16 = {0, 24576, 8699, 16393, 0, 0, 0, 0},
v4_int32 = {3.68934881e+19, 2.142699, 0, 0},
v2_int64 = {3.1415927410125732, 0},
uint128 = 1.68198862051666987877e-4932
}
pwndbg> p/f $xmm1
$6 = {
v4_float = {3.68934881e+19, 2.392699, 1.83893032e+25, 7.31235546e+28},
v2_double = {6.2831854820251465, 5.3585666837729773e+228},
v16_int8 = {0, 0, 0, 96, -5, 33, 25, 64, 98, 97, 115, 105, 99, 70, 108, 111},
v8_int16 = {0, 24576, 8699, 16409, 24930, 26995, 18019, 28524},
v4_int32 = {3.68934881e+19, 2.392699, 1.83893032e+25, 7.31235546e+28},
v2_int64 = {6.2831854820251465, 5.3585666837729773e+228},
uint128 = <invalid float value>
}
pwndbg>
Observe that the float 'vector' inside of XMM1 and XMM0 are now nonsense, because the value can no longer be
represented as a float (because it was converted to a double with the cvtss2sd instruction). OK, so
why did the compiler randomly insert those two instructions to promote the floats to doubles? This is because
when a %f format specifier is supplied to printf() any provided float values are
automatically promoted to a double! I'm sure that there's a reason for this, but I was unable to find it in my
sleuthing. If you know, or are able to find out then please let me know!
Onwards then, to the next piece of floating point number weirdness. After the two calls to cvtss2sd
we see that the "The truncated value of PI is %f and PI2 is %f\n" string is loaded into RDI and then
printf() is called immediately afterwards. It should immediately ring alarm bells in your mind that
deliciousPI and deliciousPI2 are not placed into RSI and RDX, how are they being
passed to printf as arguments? This is some unfortunate vaguely documented ASM calling convention
magic. Floating point arguments are passed to functions in the XMM0-7 registers, and the runtime is able to
somehow ascertain that those registers contain arguments to a function (as opposed to just holding transient
data.
This gets even weirder though. Consider we have hypothetical a function with this prototype
float myFunction(int arg1, float arg2, int arg3); -
- arg1 would be placed into RDI as normal
- arg2 would be placed into XMM0
- arg3 would be placed into RDX
- The return value from myFunction would be placed into XMM0
Notice how RSI (which the second argument is typically placed into) is completely skipped, because the second argument is a float. This is pretty confusing, and worth remembering if you're analyzing a function and wondering where the arguments might be. Also notice that rather than using RAX to hold the return value from the function, XMM0 is used instead, because it's capable of holding the float.
Floating point arithmetic
We have some basic knowledge about how floats are represented in ASM, so now we're able to dig in a little deeper and look at some mathematical operations.
Addition
Floating point addition is performed using the addss or addsd instructions. They take
two operands in the format addss DESTINATION, SOURCE.
Let's take a look at a small C application which adds two floats together, available in the lesson container at /lesson/floatAddition.c and /lesson/floatAdditionCompiled -
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char** argv) {
float deliciousPI = 3.1415927f;
float deliciousPI2 = 6.2831854f;
float combinedPI = deliciousPI + deliciousPI2;
printf("%f + %f = %f\n", deliciousPI, deliciousPI2, combinedPI);
exit(0);
}
Once again, very simple - it adds two floating point numbers together and then prints them. Let's disassemble the
program and see what it does. Load /lesson/floatAdditionCompiled up in GDB, set a breakpoint on
main and then run the program. Step the code with n until the first movss instruction.
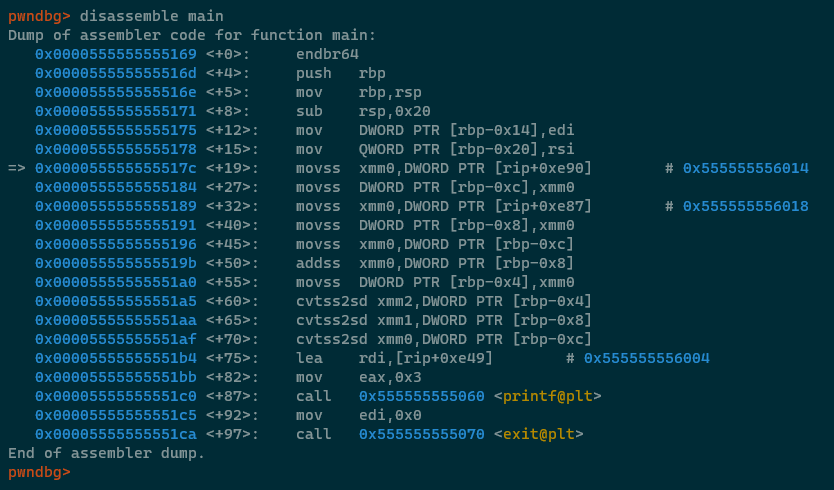
So, the first four movss instructions are hopefully familiar after looking at the floating point
basics code above; they take deliciousPI and deliciousPI's values out of the .rodata
section and place them into the current stackframe. The next movss places deliciousPI
(located at RBP-0xc) back into xmm0 and then the addss xmm0, DWORD PTR [RBP-0x8] instruction adds
deliciousPI2 to XMM0. XMM0 at this point should equal 9.424777....
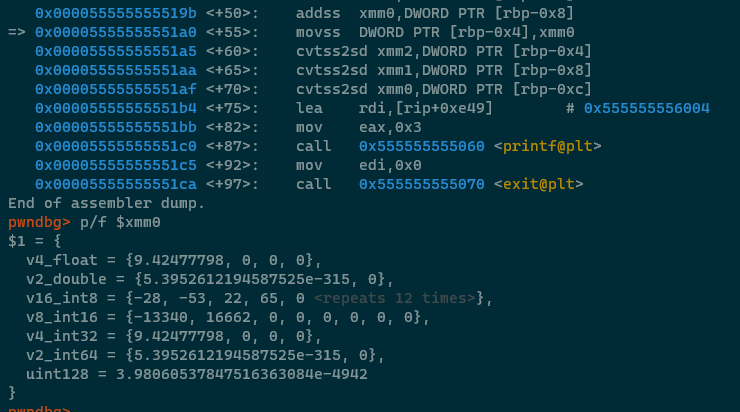
Perfect. The result is stored on the stack at RBP-0x4, the values are converted to doubles with
cvtss2sd and the values are placed into XMM0, XMM1, XMM2 ready for the call to printf
and the application subsequently exits.
Subtraction
Subtraction is virtually identical to addition except it uses the subss instruction to perform the
subtraction. The instruction format is the same, subss DESTINATION, SOURCE. An example has been
provided in the lesson's container under /lesson/floatSubtraction.c and
/lesson/floatSubtractionCompiled.
Multiplication
Multiplying floats is as painless as addition and subtraction thankfully. There are two instructions,
mulss and mulsd for multiplying floats and doubles respectively. The instructions both
take the following formats mulss destination, source and
mulss destination, source1, source2 (this one is less commonly observed in my experience). Let's
take a look at a slightly more complicated example, available in the container at
/lesson/floatMultiplication.c and /lesson/floatMultiplicationCompiled -
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char** argv) {
float value1 = 0.25;
int value2 = 4;
float value3 = value1 * value2;
printf("value3 is %f\n", value3);
float value4 = 1.23;
float value5 = 2.01;
float value6 = (((value4 * value5) + (value3 * value5)*53)-1);
printf("value6 is %f\n", value6);
exit(0);
}
Pretty ugly code, we can all agree. It multiplies value1 and value2 together into value3, which is then printed. Then it creates value6 by multiplying pairs of floats together, adding them, multiplying one side of the equation by 53 and then subtracting 1 from the resulting mess. I deliberately wrote this ugly and poorly commented piece of code because I thought that it would make the resulting ASM more interesting to analyze. The ASM:
pwndbg> disassemble
Dump of assembler code for function main:
=> 0x0000555555555169 <+0>: endbr64
0x000055555555516d <+4>: push rbp
0x000055555555516e <+5>: mov rbp,rsp
0x0000555555555171 <+8>: sub rsp,0x30
0x0000555555555175 <+12>: mov DWORD PTR [rbp-0x24],edi
0x0000555555555178 <+15>: mov QWORD PTR [rbp-0x30],rsi
0x000055555555517c <+19>: movss xmm0,DWORD PTR [rip+0xe9c] # 0x555555556020
0x0000555555555184 <+27>: movss DWORD PTR [rbp-0x18],xmm0
0x0000555555555189 <+32>: mov DWORD PTR [rbp-0x14],0x4
0x0000555555555190 <+39>: cvtsi2ss xmm0,DWORD PTR [rbp-0x14]
0x0000555555555195 <+44>: movss xmm1,DWORD PTR [rbp-0x18]
0x000055555555519a <+49>: mulss xmm0,xmm1
0x000055555555519e <+53>: movss DWORD PTR [rbp-0x10],xmm0
0x00005555555551a3 <+58>: cvtss2sd xmm0,DWORD PTR [rbp-0x10]
0x00005555555551a8 <+63>: lea rdi,[rip+0xe55] # 0x555555556004
0x00005555555551af <+70>: mov eax,0x1
0x00005555555551b4 <+75>: call 0x555555555060 <printf@plt>
0x00005555555551b9 <+80>: movss xmm0,DWORD PTR [rip+0xe63] # 0x555555556024
0x00005555555551c1 <+88>: movss DWORD PTR [rbp-0xc],xmm0
0x00005555555551c6 <+93>: movss xmm0,DWORD PTR [rip+0xe5a] # 0x555555556028
0x00005555555551ce <+101>: movss DWORD PTR [rbp-0x8],xmm0
0x00005555555551d3 <+106>: movss xmm0,DWORD PTR [rbp-0xc]
0x00005555555551d8 <+111>: movaps xmm1,xmm0
0x00005555555551db <+114>: mulss xmm1,DWORD PTR [rbp-0x8]
0x00005555555551e0 <+119>: movss xmm0,DWORD PTR [rbp-0x10]
0x00005555555551e5 <+124>: movaps xmm2,xmm0
0x00005555555551e8 <+127>: mulss xmm2,DWORD PTR [rbp-0x8]
0x00005555555551ed <+132>: movss xmm0,DWORD PTR [rip+0xe37] # 0x55555555602c
0x00005555555551f5 <+140>: mulss xmm0,xmm2
0x00005555555551f9 <+144>: addss xmm0,xmm1
0x00005555555551fd <+148>: movss xmm1,DWORD PTR [rip+0xe2b] # 0x555555556030
0x0000555555555205 <+156>: subss xmm0,xmm1
0x0000555555555209 <+160>: movss DWORD PTR [rbp-0x4],xmm0
0x000055555555520e <+165>: cvtss2sd xmm0,DWORD PTR [rbp-0x4]
0x0000555555555213 <+170>: lea rdi,[rip+0xdf8] # 0x555555556012
0x000055555555521a <+177>: mov eax,0x1
0x000055555555521f <+182>: call 0x555555555060 <printf@plt>
0x0000555555555224 <+187>: mov edi,0x0
0x0000555555555229 <+192>: call 0x555555555070 <exit@plt>
OK, the ASM samples are starting to get quite meaty and interesting at this point. Let's start off our analysis
in GDB by identifying what each of those RIP relative addresses are (ignoring the two which put values into RDI
because we know that they are strings which are passed to printf).
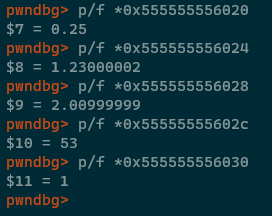
As expected, there is one constant in the .rodata section for each float value in the original C
code. Observe though how the number 4 from line 6 (value2) isn't stored in .rodata? It's instead
simply hardcoded in mov DWORD PTR [rbp-0x14],0x4, because it's an integer.
Part of my process whilst reverse engineering is to mentally keep track of stack frame offsets and their values, so let's do that quickly -
rbp-0x18==value1rbp-0x14==value2rbp-0x10== currently unknown, but we see amulssinstruction there so it's likely to bevalue3right?rbp-0xc==value4rbp-0x8==value5rbp-0x4== currently unknown, but it's placed on the stack after a slew ofaddss / subss / mulssso it's almost certainlyvalue5
This process is significantly easier when using tools like Ghidra and IDA because in those tools you can rename "variables" and add inline comments etc., we're "Learning RE The Hard Way" as Zed Shaw would say, so we don't get such fancy trappings. 😁
Let's break the ASM down chunk by chunk, starting at the first movss.
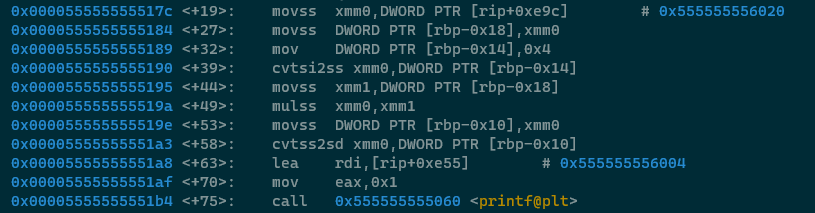
This small block of code puts value1 into XMM0, then puts it on the stack at offset RBP-0x18. It then puts the
integer 4 (value2) onto the stack at offset RBP-0x14. The next instruction though (cvtsi2ss) is new
to us, although we should be able to infer it's meaning from the explanations above - it stands for Convert
Scalar Integer To Scalar Single, AKA it casts an integer to a floating point number. At this point XMM0
contains the float representation of 1.
Next up, value1 is loaded into XMM1, which is then multiplied with XMM0 using the mulss
instruction. At this point XMM0 is the result of value1*value2 (which is value3!) this value is
then placed on the stack with movss at offset RBP-0x10. This value is then converted to a double
with cvtss2sd and used as an argument to printf(), like we've seen numerous times
above. Onto the next chunk!
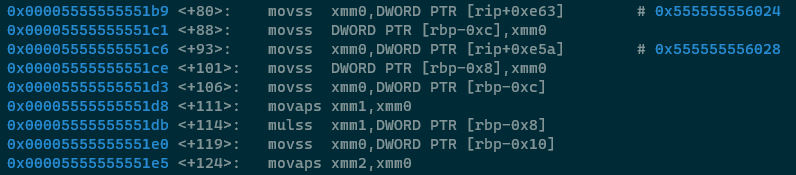
I hope that by now the first four instructions need no introduction. They load value4 and
value5 into XMM0 and then put them on the stack as described above. Next up we put
value4 into XMM0 and then we see a new instruction called movaps, which stands for Move Aligned Packed Single (float). This
instruction is almost identical to movss in that it is able to manipulate/interact with the XMM
registers, but the distinction is that it copies the entire state of the register to a destination, rather than
simply copying a single scalar (a float) out of the register. So this instruction essentially clones XMM0 into
XMM1, just on the off chance that XMM0 contained multiple floats/doubles/ints.
Next up, value5 is multiplied with XMM1 which concludes the (value4 * value5) part of
the equation. The code block ends with value3being placed into XMM2.
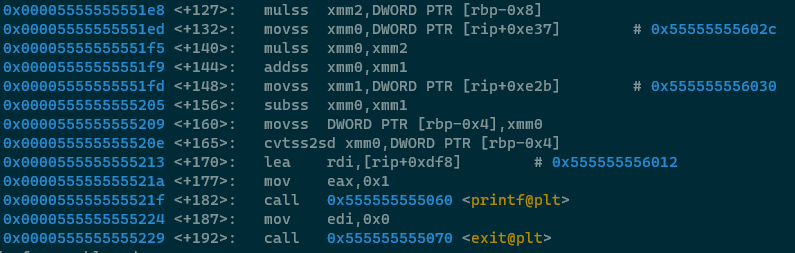
Next up, value3 and value5 get multiplied together, '53' is moved into XMM0 using a RIP
relative fetch and then that value is multiplied with the result of (value3 * value5). The result
of that multiplication is added to the result of the multiplication operations in the chunk above 👆, then '1'
is put into XMM1 using a RIP relative fetch again, and that value is subtracted from the overall result of all
of the multiplications. The final value is put on the stack at RBP-4 and then printed as usual.
This was probably our most involved code sample yet, I hope that it was useful to step through it chunk by chunk in such a fashion - this approach to reverse engineering is beneficial even when source code is not available. Select arbitrary 'chunks' of a piece of function disassembly and work through them piece by piece to develop a picture of what's occurring. Eventually you'll be able to just intuitively disregard the 'noise' (irrelevant fluff) and only see the 'signal' (important stuff).
Division
OK we're getting towards the end of this lesson now - one mathematical operation left to cover, division. Recall in the mathematics lesson that integer division was confusing and flakey arcane sorcery? Float division is nothing like that, thankfully.
Division is performed using one of two instructions, divss for floats and divsd for
doubles. Here's a basic example of float division from /lesson/floatDivision.c and
/lesson/floatDivisionCompiled. The C code -
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char** argv) {
float value1 = 117.25;
float value2 = 4.17;
float value3 = value1 / value2;
printf("value3 is %f\n", value3);
exit(0);
}
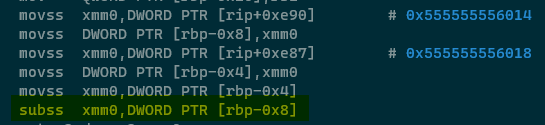
Simple stuff, two float values are created, divided and then printed. Let's see the resulting ASM -
pwndbg> disassemble
Dump of assembler code for function main:
=> 0x0000555555555169 <+0>: endbr64
0x000055555555516d <+4>: push rbp
0x000055555555516e <+5>: mov rbp,rsp
0x0000555555555171 <+8>: sub rsp,0x20
0x0000555555555175 <+12>: mov DWORD PTR [rbp-0x14],edi
0x0000555555555178 <+15>: mov QWORD PTR [rbp-0x20],rsi
0x000055555555517c <+19>: movss xmm0,DWORD PTR [rip+0xe90] # 0x555555556014
0x0000555555555184 <+27>: movss DWORD PTR [rbp-0xc],xmm0
0x0000555555555189 <+32>: movss xmm0,DWORD PTR [rip+0xe87] # 0x555555556018
0x0000555555555191 <+40>: movss DWORD PTR [rbp-0x8],xmm0
0x0000555555555196 <+45>: movss xmm0,DWORD PTR [rbp-0xc]
0x000055555555519b <+50>: divss xmm0,DWORD PTR [rbp-0x8]
0x00005555555551a0 <+55>: movss DWORD PTR [rbp-0x4],xmm0
0x00005555555551a5 <+60>: cvtss2sd xmm0,DWORD PTR [rbp-0x4]
0x00005555555551aa <+65>: lea rdi,[rip+0xe53] # 0x555555556004
0x00005555555551b1 <+72>: mov eax,0x1
0x00005555555551b6 <+77>: call 0x555555555060 <printf@plt>
0x00005555555551bb <+82>: mov edi,0x0
0x00005555555551c0 <+87>: call 0x555555555070 <exit@plt>
All very simple stuff I expect after the absolute onslaught of information in this lesson! Constants are pulled
from .rodata using a RIP relative fetch, stored on the stack at RBP-0xC and RBP-0x8, then the values are divided
using the divss instruction. Step through the code using n and inspect the contents of
XMM0 before and after the division -
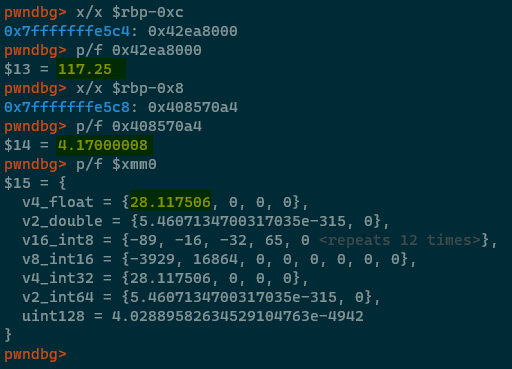
Observe how the singular divss instruction was able to correctly divide the two float values to a
high degree of precision, without needing to cram data into any other registers, and without requiring any other
strange instructions like CDQ to allow execution to continue? Just wonderful.
Conclusion
This has been a long and intense lesson. As I noted above, I was dreading writing this lesson up because floats are kind of frustrating and introduce a lot of (initially) confusing and difficult to read mnemonics. Also interacting with the XMM registers in GDB is a little painful too unfortunately - running i r sse and i r xmm0 show the registers but don't show you the values as floats for some reason (the values are rounded to whole integers).
At this point in the course, we've covered all of the basics of the x64 assembly language. As a reader, you should now be able to analyze binaries which contain the following functionality:
- Multiple functions
- Integer and floating point arithmetic
- Conditional statements
- Iteration via
for/do/whileloops - Bitwise logic
This is my tongue in cheek way of indicating that you can now analyze virtually any binary, because you should understand the fundamental building blocks of any application! This field is vast though and it's important to keep growing, so in order to keep on learning and improving at this point I'd suggest the following steps -
- Work through the challenge binaries which I've created at /x64_challenges
- Start working through some `crackme` challenges from crackmes.one
- Continue with the methodology that this site instilled by writing your own apps and disassembling them yourself
- Malware analysis.
- Be very careful with this one though of course, setup an airgapped and isolated environment to do this so you don't pwn your machine.
Thanks so much for reading, I hope that this material has been as fun to read as it was to write.